Mathematics - Real Life | Maths 7th STd
Untitled
Chapter 2
Fractions and Decimals
2.1 Introduction
You have learnt fractions and decimals in earlier classes. The study of fractions included proper, improper and mixed fractions as well as their addition and subtraction. We also studied comparison of fractions, equivalent fractions, representation of fractions on the number line and ordering of fractions.
Our study of decimals included, their comparison, their representation on the number line and their addition and subtraction.
We shall now learn multiplication and division of fractions as well as of decimals.
2.2 How Well have You Learnt about Fractions?
A proper fraction is a fraction that represents a part of a whole. Is 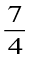 a proper fraction? Which is bigger, the numerator or the denominator?
a proper fraction? Which is bigger, the numerator or the denominator?
An improper fraction is a combination of whole and a proper fraction. Is 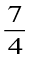 an improper fraction? Which is bigger here, the numerator or the denominator?
an improper fraction? Which is bigger here, the numerator or the denominator?
The improper fraction 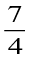 can be written as
can be written as 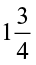 . This is a mixed fraction.
. This is a mixed fraction.
Can you write five examples each of proper, improper and mixed fractions?
Example 1 Write five equivalent fractions of  .
.
Solution One of the equivalent fractions of  is
is
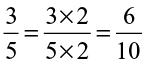 . Find the other four.
. Find the other four.
Example 2 Ramesh solved  part of an exercise while Seema solved
part of an exercise while Seema solved 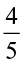 of it. Who solved lesser part?
of it. Who solved lesser part?
In order to find who solved lesser part of the exercise, let us compare 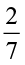 and
and 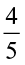 .
.

Converting them to like fractions we have, 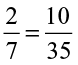 ,
, 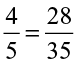 .
.
Since 10 < 28 , so 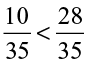 .
.
Thus, 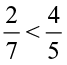 .
.
Ramesh solved lesser part than Seema.
Example 3 Sameera purchased 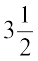 kg apples and
kg apples and 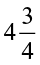 kg oranges. What is the total weight of fruits purchased by her?
kg oranges. What is the total weight of fruits purchased by her?
Solution The total weight of the fruits 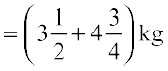
 =
= 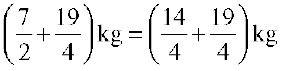
= 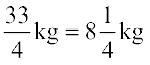
Example 4 Suman studies for 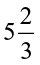 hours daily. She devotes
hours daily. She devotes  hours of her time for Science and Mathematics. How much time does she devote for other subjects?
hours of her time for Science and Mathematics. How much time does she devote for other subjects?
Solution Total time of Suman’s study = 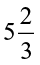 h =
h = 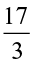 h
h
 Time devoted by her for Science and Mathematics =
Time devoted by her for Science and Mathematics = 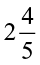 =
= 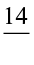 h
h
Thus, time devoted by her for other subjects = 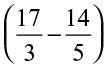 h
h
= 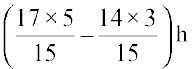 =
= 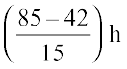 =
= 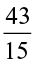 h =
h = 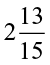 h
h
Exercise 2.1
 1. Solve:
1. Solve:
(i) 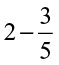 (ii)
(ii) 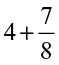 (iii)
(iii) 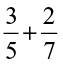 (iv)
(iv) 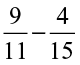
(v) 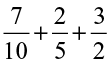 (vi)
(vi)  (vii)
(vii) 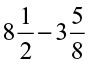
2. Arrange the following in descending order:
(i)  (ii)
(ii) 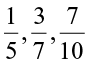 .
.
3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
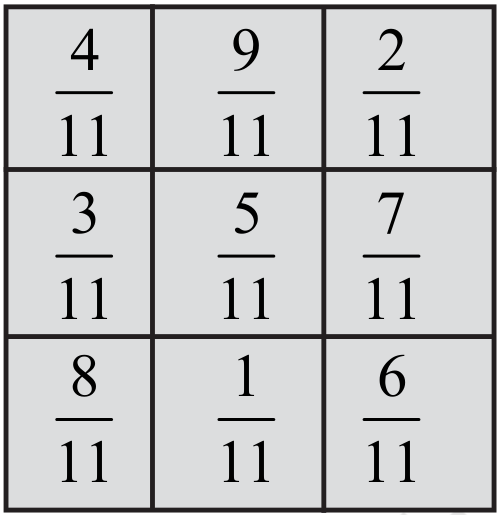
(Along the first row 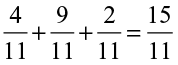 ).
).
4. A rectangular sheet of paper is 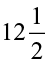 cm long and
cm long and 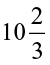 cm wide. Find its perimeter.
cm wide. Find its perimeter.
5. Find the perimeters of (i) ∆ ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
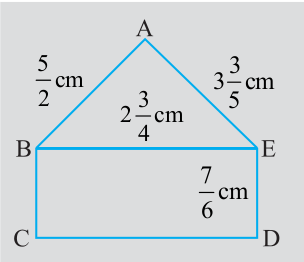
6. Salil wants to put a picture in a frame. The picture is 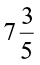 cm wide. To fit in the frame the picture cannot be more than
cm wide. To fit in the frame the picture cannot be more than 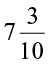 cm wide. How much should the picture be trimmed?
cm wide. How much should the picture be trimmed?
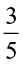 part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
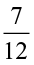 hour. Vaibhav finished colouring the same picture in
hour. Vaibhav finished colouring the same picture in 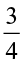 hour. Who worked longer? By what fraction was it longer?
hour. Who worked longer? By what fraction was it longer?
2.3 Multiplication of Fractions
You know how to find the area of a rectangle. It is equal to length × breadth. If the length and breadth of a rectangle are 7 cm and 4 cm respectively, then what will be its area? Its area would be 7 × 4 = 28 cm2.
What will be the area of the rectangle if its length and breadth are  cm and
cm and  cm respectively? You will say it will be
cm respectively? You will say it will be 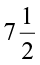 ×
× 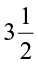 =
= 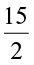 ×
× 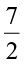 cm2. The numbers
cm2. The numbers 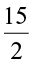 and
and 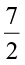 are fractions. To calculate the area of the given rectangle, we need to know how to multiply fractions. We shall learn that now.
are fractions. To calculate the area of the given rectangle, we need to know how to multiply fractions. We shall learn that now.
2.3.1 Multiplication of a Fraction by a Whole Number
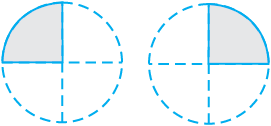
Fig 2.1
Observe the pictures at the left (Fig 2.1). Each shaded part is 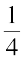 part of a circle. How much will the two shaded parts represent together? They will represent
part of a circle. How much will the two shaded parts represent together? They will represent 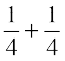 =
= 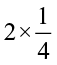 .
.
Combining the two shaded parts, we get Fig 2.2 . What part of a circle does the shaded part in Fig 2.2 represent? It represents 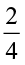 part of a circle .
part of a circle .
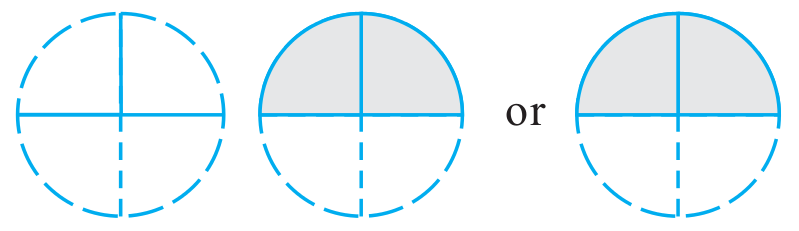
Fig 2.2
The shaded portions in Fig 2.1 taken together are the same as the shaded portion in Fig 2.2, i.e., we get Fig 2.3.

Fig 2.3
or  =
= 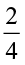 .
.
Can you now tell what this picture will represent? (Fig 2.4)

Fig 2.4
And this? (Fig 2.5)

Fig 2.5
Let us now find 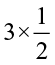 .
.
We have 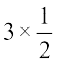 =
= 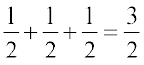
We also have 
So 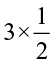 =
= 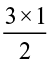 =
= 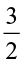
Similarly  =
= 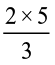 = ?
= ?
Can you tell 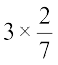 = ?
= ? 
The fractions that we considered till now, i.e., 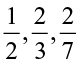 and
and 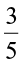 were proper fractions.
were proper fractions.
For improper fractions also we have,
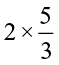 =
= 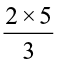 =
= 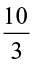
Try, 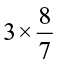 = ?
= ?  = ?
= ?
Thus, to multiply a whole number with a proper or an improper fraction, we multiply the whole number with the numerator of the fraction, keeping the denominator same.
Try These

1. Find: (a) 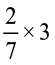 (b)
(b) 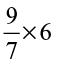 (c)
(c) 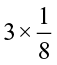 (d)
(d) 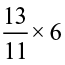
If the product is an improper fraction express it as a mixed fraction.
2. Represent pictorially : 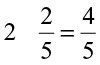
Try These
 Find: (i)
Find: (i) 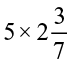
(ii) 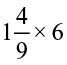

To multiply a mixed fraction to a whole number, first convert the mixed fraction to an improper fraction and then multiply.
Therefore, 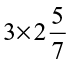 =
= 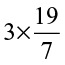 =
= 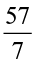 =
= 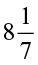 .
.
Similarly, 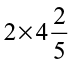 =
= 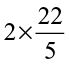 = ?
= ?
Fraction as an operator ‘of’
Observe these figures (Fig 2.6)
The two squares are exactly similar.
Each shaded portion represents  of 1.
of 1.
So, both the shaded portions together will represent 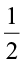 of 2.
of 2.
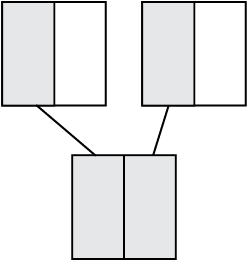
Combine the 2 shaded 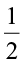 parts. It represents 1.
parts. It represents 1.
So, we say 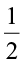 of 2 is 1. We can also get it as
of 2 is 1. We can also get it as 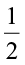 × 2 = 1.
× 2 = 1.
Thus, 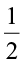 of 2 =
of 2 = 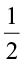 × 2 = 1
× 2 = 1
Also, look at these similar squares (Fig 2.7).
Each shaded portion represents  of 1.
of 1.
So, the three shaded portions represent 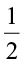 of 3.
of 3.
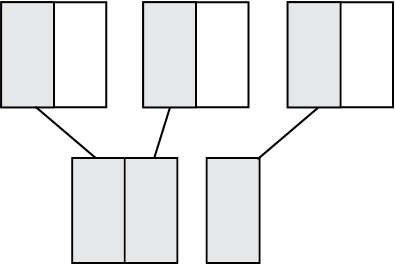
Fig 2.7
Combine the 3 shaded parts.
It represents 1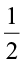 i.e.,
i.e., 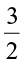 .
.
So,  of 3 is
of 3 is 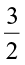 . Also,
. Also, 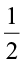 × 3 =
× 3 =  .
.
Thus, 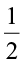 of 3 =
of 3 = 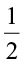 × 3 =
× 3 = 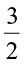 .
.
So we see that ‘of’ represents multiplication.
Farida has 20 marbles. Reshma has 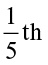 of the number of marbles what Farida has. How many marbles Reshma has? As, ‘of’ indicates multiplication, so, Reshma has
of the number of marbles what Farida has. How many marbles Reshma has? As, ‘of’ indicates multiplication, so, Reshma has 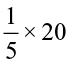 = 4 marbles.
= 4 marbles.

Similarly, we have  of 16 is
of 16 is 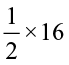 =
= 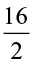 = 8.
= 8.
Try These

Can you tell, what is (i) 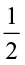 of 10?, (ii)
of 10?, (ii) 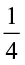 of 16?, (iii)
of 16?, (iii) 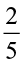 of 25?
of 25?
Example 5 In a class of 40 students 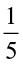 of the total number of studetns like to study English,
of the total number of studetns like to study English, 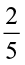 of the total number like to study Mathematics and the remaining students like to study Science.
of the total number like to study Mathematics and the remaining students like to study Science.
(i) How many students like to study English?
(ii) How many students like to study Mathematics?
(iii) What fraction of the total number of students like to study Science?
Solution Total number of students in the class = 40.
(i) Of these 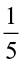 of the total number of students like to study English.
of the total number of students like to study English.
Thus, the number of students who like to study English = 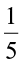 of 40 =
of 40 = 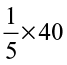 = 8.
= 8.
(ii) Try yourself.
(iii) The number of students who like English and Mathematics = 8 + 16 = 24. Thus, the number of students who like Science = 40 – 24 = 16.
Thus, the required fraction is 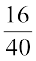 .
.
Exercise 2.2

1. Which of the drawings (a) to (d) show :
(i) 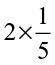 (ii)
(ii) 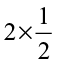 (iii)
(iii) 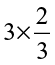 (iv)
(iv) 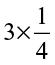
(a) 
(b) 
(c) 
(d) 
2. Some pictures (a) to (c) are given below. Tell which of them show:
(i) 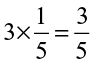 (ii)
(ii) 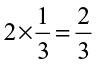 (iii)
(iii) 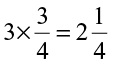
(a) 
(b) 
(c) 
3. Multiply and reduce to lowest form and convert into a mixed fraction:
(i)  (ii)
(ii) 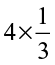 (iii)
(iii) 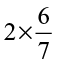 (iv)
(iv) 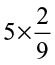 (v)
(v) 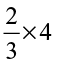
(vi) 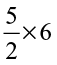 (vii)
(vii) 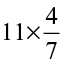 (viii)
(viii) 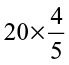 (ix)
(ix) 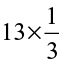 (x)
(x) 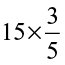
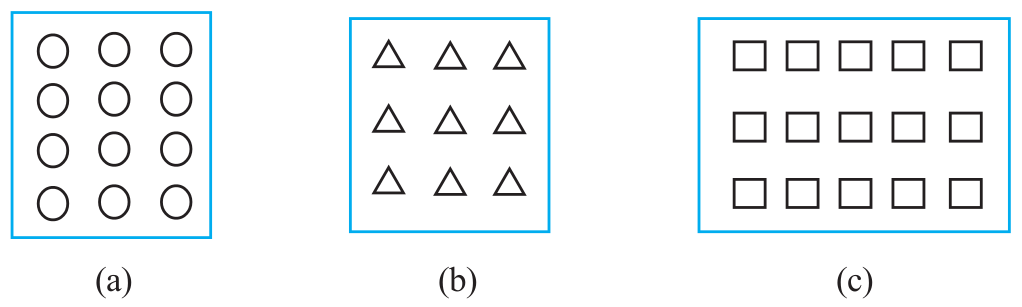
4. Shade: (i) 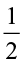 of the circles in box (a) (ii)
of the circles in box (a) (ii) 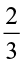 of the triangles in box (b)
of the triangles in box (b)
(iii) 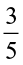 of the squares in box (c).
of the squares in box (c).
5. Find:
(a) 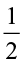 of (i) 24 (ii) 46 (b)
of (i) 24 (ii) 46 (b) 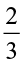 of (i) 18 (ii) 27
of (i) 18 (ii) 27
(c)  of (i) 16 (ii) 36 (d)
of (i) 16 (ii) 36 (d) 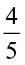 of (i) 20 (ii) 35
of (i) 20 (ii) 35
6. Multiply and express as a mixed fraction :

(a) 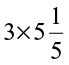 (b)
(b) 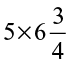 (c)
(c) 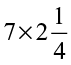 (d)
(d) 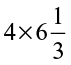
(e) 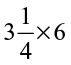 (f)
(f) 
7. Find: (a) 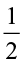 of (i)
of (i) 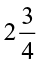 (ii)
(ii) 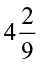 (b)
(b) 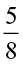 of (i)
of (i) 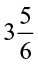 (ii)
(ii) 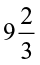
8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed 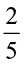 of the water. Pratap consumed the remaining water.
of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
2.3.2 Multiplication of a Fraction by a Fraction
Farida had a 9 cm long strip of ribbon. She cut this strip into four equal parts. How did she do it? She folded the strip twice. What fraction of the total length will each part represent? Each part will be 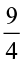 of the strip. She took one part and divided it in two equal parts by folding the part once. What will one of the pieces represent? It will represent
of the strip. She took one part and divided it in two equal parts by folding the part once. What will one of the pieces represent? It will represent 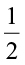 of
of 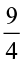 or
or 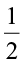 ×
× 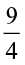 .
.
Let us now see how to find the product of two fractions like 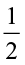 ×
× 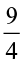 .
.
To do this we first learn to find the products like 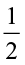 ×
× 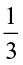 .
.

Fig 2.8
(a) How do we find 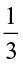 of a whole? We divide the whole in three equal parts. Each of the three parts represents
of a whole? We divide the whole in three equal parts. Each of the three parts represents 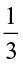 of the whole. Take one part of these three parts, and shade it as shown in Fig 2.8.
of the whole. Take one part of these three parts, and shade it as shown in Fig 2.8.
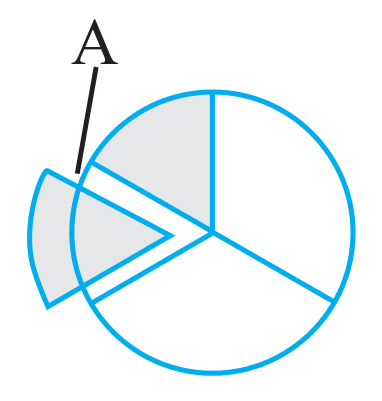
Fig 2.9
(b) How will you find 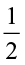 of this shaded part? Divide this one-third (
of this shaded part? Divide this one-third (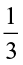 ) shaded part into two equal parts. Each of these two parts represents
) shaded part into two equal parts. Each of these two parts represents 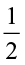 of
of 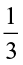 i.e.,
i.e., 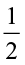 ×
×  (Fig 2.9).
(Fig 2.9).
Take out 1 part of these two and name it ‘A’. ‘A’ represents 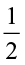 ×
× 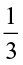 .
.
(c) What fraction is ‘A’ of the whole? For this, divide each of the remaining 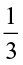 parts also in two equal parts. How many such equal parts do you have now?
parts also in two equal parts. How many such equal parts do you have now?
There are six such equal parts. ‘A’ is one of these parts.
So, ‘A’ is 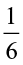 of the whole. Thus,
of the whole. Thus,  ×
× 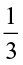 =
= 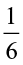 .
.
How did we decide that ‘A’ was 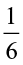 of the whole? The whole was divided in 6 = 2 × 3 parts and 1 = 1 × 1 part was taken out of it.
of the whole? The whole was divided in 6 = 2 × 3 parts and 1 = 1 × 1 part was taken out of it.
Thus,  ×
× 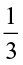 =
= 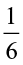 =
= 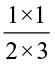
or  ×
× 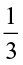 =
= 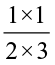
The value of 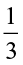 ×
×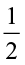 can be found in a similar way. Divide the whole into two equal parts and then divide one of these parts in three equal parts. Take one of these parts. This will represent
can be found in a similar way. Divide the whole into two equal parts and then divide one of these parts in three equal parts. Take one of these parts. This will represent 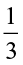 ×
× 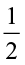 i.e.,
i.e., 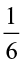 .
.
Therefore 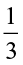 ×
× 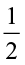 =
= 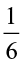 =
= 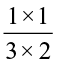 as discussed earlier.
as discussed earlier.
Hence 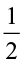 ×
× 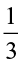 =
= 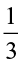 ×
× 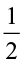 =
= 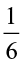
Find 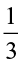 ×
×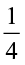 and
and 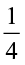 ×
× 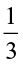 ;
; 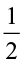 ×
×  and
and  ×
× 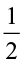 and check whether you get
and check whether you get
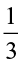 ×
×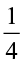 =
= 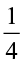 ×
× 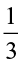 ;
; 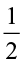 ×
× 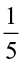 =
= 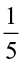 ×
× 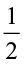
Try These
Fill in these boxes:
(i) 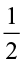 ×
× 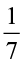 =
= 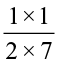 =
=  (ii)
(ii) 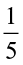 ×
× 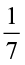 =
=  =
= 
(iii) 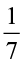 ×
× 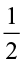 =
=  =
=  (iv)
(iv) 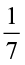 ×
× 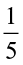 =
=  =
= 
Example 6 Sushant reads  part of a book in 1 hour. How much part of the book will he read in
part of a book in 1 hour. How much part of the book will he read in 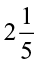 hours?
hours?
Solution The part of the book read by Sushant in 1 hour =  .
.
 So, the part of the book read by him in
So, the part of the book read by him in 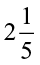 hours =
hours = 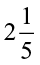 ×
× 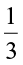
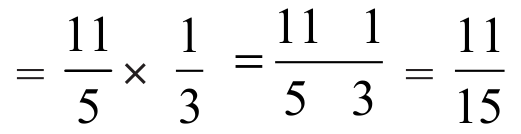
Let us now find 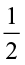 ×
×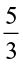 . We know that
. We know that 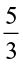 =
= 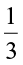 × 5 .
× 5 .
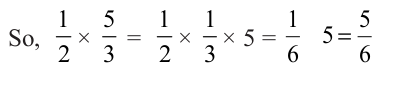
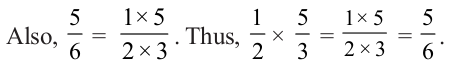
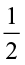 ×
× 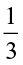 =
= 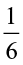 . The total of such parts would be 5 ×
. The total of such parts would be 5 ×  =
= 
 .
.
Try These

Find: 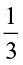 ×
×  ;
; 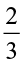 ×
× 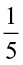
Similarly  =
= 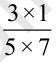 =
= 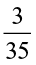
We can thus find 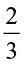 ×
× 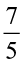 as
as 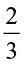 ×
× 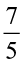 =
=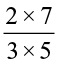 =
= 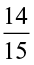 .
.
So, we find that we multiply two fractions as  .
.
Value of the Products
You have seen that the product of two whole numbers is bigger than each of the two whole numbers. For example, 3 × 4 = 12 and 12 > 4, 12 > 3. What happens to the value of the product when we multiply two fractions?
Let us first consider the product of two proper fractions.
Try These
Find: 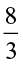 ×
×  ;
; 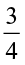 ×
× 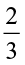 .
.
We have,
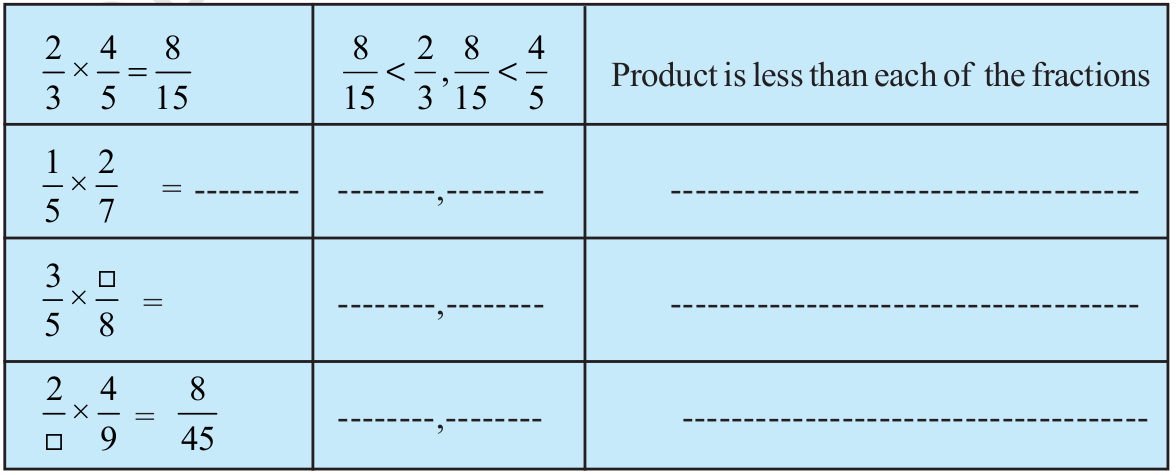
You will find that when two proper fractions are multiplied, the product is less than each of the fractions. Or, we say the value of the product of two proper fractions is smaller than each of the two fractions.
Check this by constructing five more examples.
Let us now multiply two improper fractions.

We find that the product of two improper fractions is greater than each of the two fractions.
Or, the value of the product of two improper fractions is more than each of the two fractions.
Construct five more examples for yourself and verify the above statement.
Let us now multiply a proper and an improper fraction, say 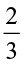 and
and 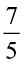 .
.
We have 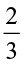 ×
×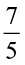 =
=  . Here,
. Here,  <
< 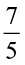 and
and  >
> 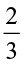
The product obtained is less than the improper fraction and greater than the proper fraction involved in the multiplication.
Check it for 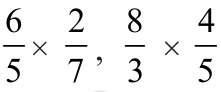 .
.
Exercise 2.3
 1. Find:
1. Find:
(i) 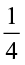 of (a)
of (a) 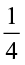 (b)
(b)  (c)
(c) 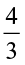
(ii) 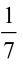 of (a)
of (a) 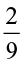 (b)
(b) 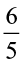 (c)
(c) 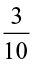
2. Multiply and reduce to lowest form (if possible) :
(i)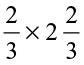 (ii)
(ii)  (iii)
(iii) 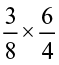 (iv)
(iv) 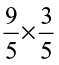
(v) 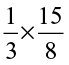 (vi)
(vi) 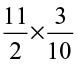 (vii)
(vii) 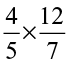
3. Multiply the following fractions:
(i) 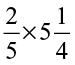 (ii)
(ii) 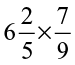 (iii)
(iii) 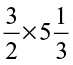 (iv)
(iv) 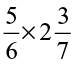
(v) 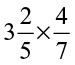 (vi)
(vi) 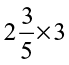 (vii)
(vii) 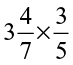
4. Which is greater:
(i)  of
of 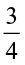 or
or 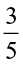 of
of 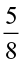 (ii)
(ii) 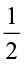 of
of 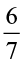 or
or 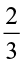 of
of 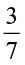
5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is 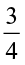 m. Find the distance between the first and the last sapling.
m. Find the distance between the first and the last sapling.
6. Lipika reads a book for 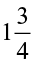 hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using 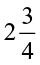 litres of petrol.
litres of petrol.
8. (a) (i) Provide the number in the box  , such that
, such that  .
.
(ii) The simplest form of the number obtained in  is _____.
is _____.

(b) (i) Provide the number in the box  , such that
, such that 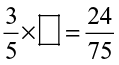 .
.
(ii) The simplest form of the number obtained in  is _____.
is _____.
2.4 Division of Fractions
John has a paper strip of length 6 cm. He cuts this strip in smaller strips of length 2 cm each. You know that he would get 6 ÷ 2 =3 strips.
John cuts another strip of length 6 cm into smaller strips of length 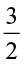 cm each. How many strips will he get now? He will get 6 ÷
cm each. How many strips will he get now? He will get 6 ÷ 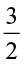 strips.
strips.
A paper strip of length 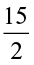 cm can be cut into smaller strips of length
cm can be cut into smaller strips of length 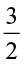 cm each to give
cm each to give 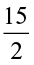 ÷
÷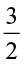 pieces.
pieces.
So, we are required to divide a whole number by a fraction or a fraction by another fraction. Let us see how to do that.
2.4.1 Division of Whole Number by a Fraction
Let us find 1÷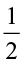 .
.
We divide a whole into a number of equal parts such that each part is half of the whole. The number of such half (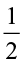 ) parts would be 1÷
) parts would be 1÷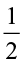 . Observe the figure (Fig 2.11). How many half parts do you see?
. Observe the figure (Fig 2.11). How many half parts do you see?
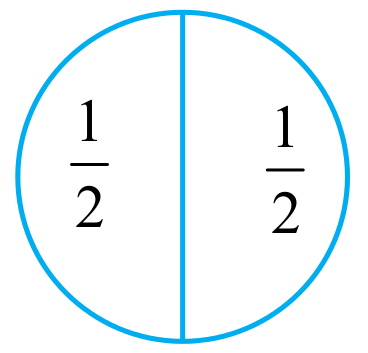
Fig 2.11
There are two half parts.
So, 1 ÷ 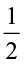 = 2. Also,
= 2. Also, 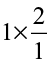 = 1 × 2 = 2. Thus, 1 ÷
= 1 × 2 = 2. Thus, 1 ÷ 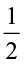 = 1 ×
= 1 × 
Similarly, 3 ÷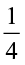 = number of
= number of 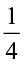 parts obtained when each of the 3 whole, are divided into
parts obtained when each of the 3 whole, are divided into 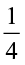 equal parts = 12 (From Fig 2.12)
equal parts = 12 (From Fig 2.12)



Fig 2.12
 Observe also that,
Observe also that, 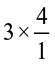 = 3 × 4 = 12. Thus,
= 3 × 4 = 12. Thus, 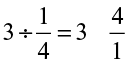 = 12.
= 12.
Find in a similar way, 3 ÷ 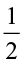 and
and 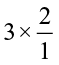 .
.
Reciprocal of a fraction
The number 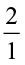 can be obtained by interchanging the numerator and denominator of
can be obtained by interchanging the numerator and denominator of 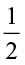 or by inverting
or by inverting 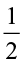 . Similarly,
. Similarly, 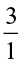 is obtained by inverting
is obtained by inverting 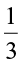 .
.
Let us first see about the inverting of such numbers.
Observe these products and fill in the blanks :
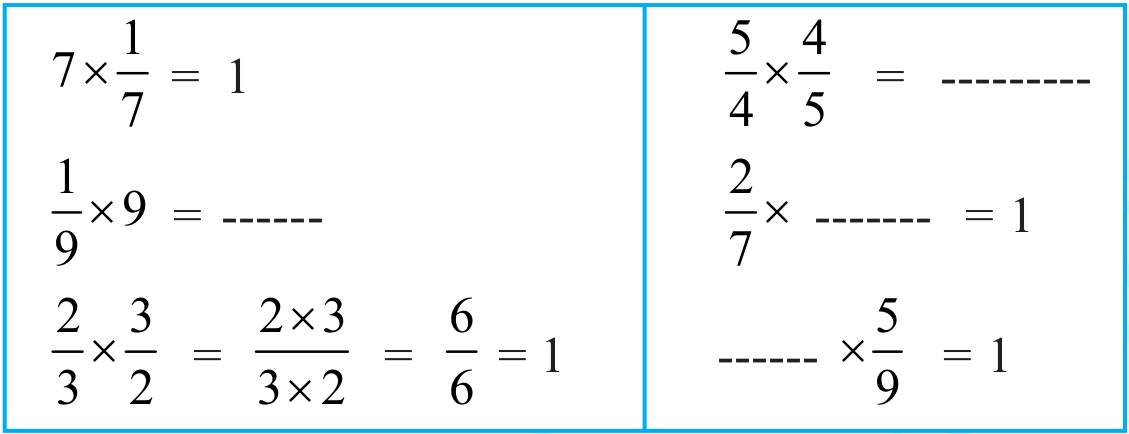
Multiply five more such pairs.
The non-zero numbers whose product with each other is 1, are called the reciprocals of each other. So reciprocal of 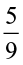 is
is 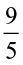 and the reciprocal of
and the reciprocal of 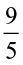 is
is 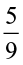 . What is the receiprocal of
. What is the receiprocal of 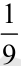 ?
? 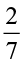 ?
?
You will see that the reciprocal of 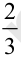 is obtained by inverting it. You get
is obtained by inverting it. You get  .
.
Think, Discuss and Write
 (i) Will the reciprocal of a proper fraction be again a proper fraction?
(i) Will the reciprocal of a proper fraction be again a proper fraction?
(ii) Will the reciprocal of an improper fraction be again an improper fraction?
Therefore, we can say that
1 ÷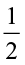 =
= 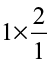 = 1× reciprocal of
= 1× reciprocal of 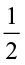 .
.
 3 ÷
3 ÷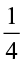 =
= 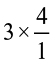 = 3× reciprocal of
= 3× reciprocal of 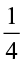 .
.
3 ÷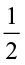 = ------ = ----------------------.
= ------ = ----------------------.
So, 2 ÷ 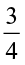 = 2 × reciprocal of
= 2 × reciprocal of 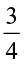 =
=  .
.
5 ÷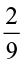 = 5 × ------------------- = 5 × -------------
= 5 × ------------------- = 5 × -------------
Thus, to divide a whole number by any fraction, multiply that whole number by the reciprocal of that fraction.
Try These
 Find : (i) 7 ÷
Find : (i) 7 ÷ 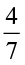 (ii) 6 ÷
(ii) 6 ÷ 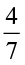 (iii) 2 ÷
(iii) 2 ÷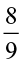
• While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and then solve it.
Thus, 4 ÷ 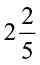 = 4 ÷
= 4 ÷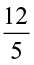 = ? Also, 5 ÷ 3
= ? Also, 5 ÷ 3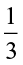 = 3 ÷
= 3 ÷ 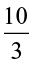 = ?
= ?
Try These
Find: (i) 6 ÷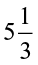
(ii) 7 ÷ 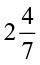
2.4.2 Division of a Fraction by a Whole Number
• What will be 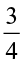 ÷ 3?
÷ 3?
Based on our earlier observations we have: 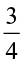 ÷ 3 =
÷ 3 = 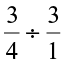 =
= 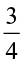 ×
× 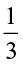 =
=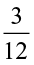 =
= 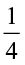
So, 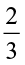 ÷ 7 =
÷ 7 = 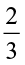 ×
× 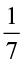 = ? What is
= ? What is 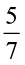 ÷ 6 ,
÷ 6 , 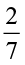 ÷ 8 ?
÷ 8 ?
• While dividing mixed fractions by whole numbers, convert the mixed fractions into improper fractions. That is,
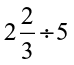 =
= 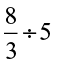 = ------ ;
= ------ ; 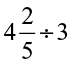 = ------ = ------;
= ------ = ------;  = ------ = ------
= ------ = ------
2.4.3 Division of a Fraction by Another Fraction
We can now find 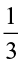 ÷
÷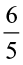 .
.
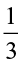 ÷
÷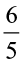 =
=  × reciprocal of
× reciprocal of  =
= 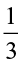 ×
× 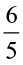 =
=  .
.
Similarly, 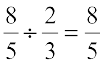 reciprocal of
reciprocal of  = ? and,
= ? and, 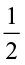 ÷
÷ 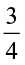 = ?
= ?
Try These

Find: (i) 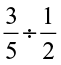 (ii)
(ii) 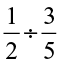 (iii)
(iii) 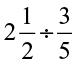 (iv)
(iv) 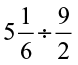
Exercise 2.4
1. Find:
(i) 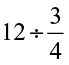 (ii)
(ii) 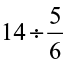 (iii)
(iii)  (iv)
(iv) 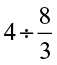
(v) 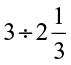 (vi)
(vi) 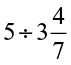
2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i)  (ii)
(ii) 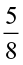 (iii)
(iii)  (iv)
(iv) 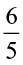
(v) 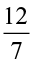 (vi)
(vi) 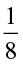 (vii)
(vii) 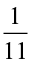
3. Find:
(i) 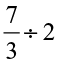 (ii)
(ii) 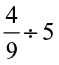 (iii)
(iii)  (iv)
(iv) 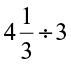
(v) 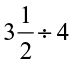 (vi)
(vi) 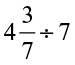
4. Find:
(i) 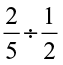 (ii)
(ii)  (iii)
(iii) 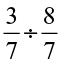 (iv)
(iv) 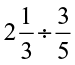 (v)
(v) 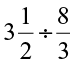
(vi) 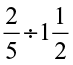 (vii)
(vii) 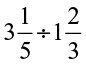 (viii)
(viii) 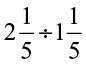
2.5 How Well have you Learnt about Decimal Numbers
You have learnt about decimal numbers in the earlier classes. Let us briefly recall them here. Look at the following table and fill up the blank spaces.
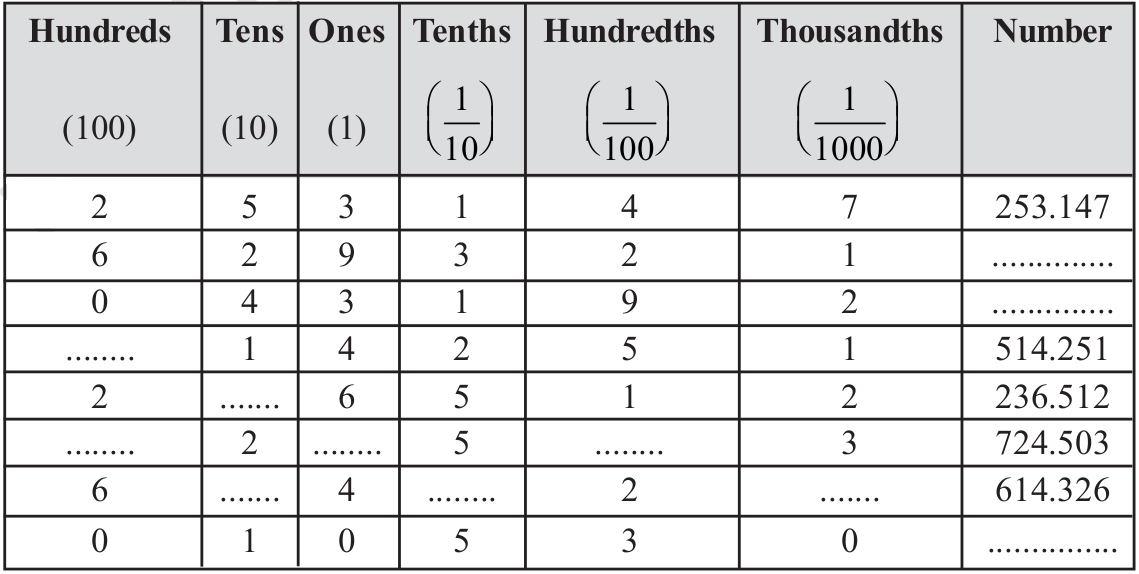
In the table, you wrote the decimal number, given its place-value expansion. You can do the reverse, too. That is, given the number you can write its expanded form. For example, 253.417 = 2 × 100 + 5 × 10 + 3 × 1 + 4 × 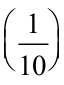 + 1 ×
+ 1 ×  + 7 ×
+ 7 × 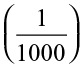 .
.
John has 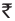 15.50 and Salma has
15.50 and Salma has 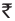 15.75. Who has more money? To find this we need to compare the decimal numbers 15.50 and 15.75. To do this, we first compare the digits on the left of the decimal point, starting from the leftmost digit. Here both the digits 1 and 5, to the left of the decimal point, are same. So we compare the digits on the right of the decimal point starting from the tenths place. We find that 5 < 7, so we say
15.75. Who has more money? To find this we need to compare the decimal numbers 15.50 and 15.75. To do this, we first compare the digits on the left of the decimal point, starting from the leftmost digit. Here both the digits 1 and 5, to the left of the decimal point, are same. So we compare the digits on the right of the decimal point starting from the tenths place. We find that 5 < 7, so we say
15.50 < 15.75. Thus, Salma has more money than John.
If the digits at the tenths place are also same then compare the digits at the hundredths place and so on.
Now compare quickly, 35.63 and 35.67; 20.1 and 20.01; 19.36 and 29.36.
While converting lower units of money, length and weight, to their higher units, we are required to use decimals. For example, 3 paise = 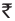
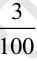 =
= 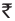 0.03, 5g =
0.03, 5g = 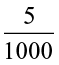 kg
kg
= 0.005 kg, 7 cm = 0.07 m.
Write 75 paise = 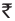 ______, 250 g = _____ kg, 85 cm = _____m.
______, 250 g = _____ kg, 85 cm = _____m.
We also know how to add and subtract decimals. Thus, 21.36 + 37.35 is
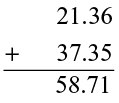
What is the value of 0.19 + 2.3 ?
The difference 29.35 − 4.56 is
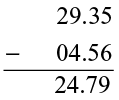
Tell the value of 39.87 − 21.98.
Exercise 2.5

1. Which is greater?
(i) 0.5 or 0.05 (ii) 0.7 or 0.5 (iii) 7 or 0.7
(iv) 1.37 or 1.49 (v) 2.03 or 2.30 (vi) 0.8 or 0.88.
2. Express as rupees using decimals :
(i) 7 paise (ii) 7 rupees 7 paise (iii) 77 rupees 77 paise
(iv) 50 paise (v) 235 paise.
3. (i) Express 5 cm in metre and kilometre (ii) Express 35 mm in cm, m and km
4. Express in kg:
(i) 200 g (ii) 3470 g (iii) 4 kg 8 g
5. Write the following decimal numbers in the expanded form:
(i) 20.03 (ii) 2.03 (iii) 200.03 (iv) 2.034
6. Write the place value of 2 in the following decimal numbers:
(i) 2.56 (ii) 21.37 (iii) 10.25 (iv) 9.42 (v) 63.352.
7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?

8. Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
9. How much less is 28 km than 42.6 km?
2.6 Multiplication of Decimal Numbers

Reshma purchased 1.5kg vegetable at the rate of 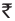 8.50 per kg. How much money should she pay? Certainly it would be
8.50 per kg. How much money should she pay? Certainly it would be 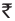 (8.50 × 1.50). Both 8.5 and 1.5 are decimal numbers. So, we have come across a situation where we need to know how to multiply two decimals. Let us now learn the multiplication of two decimal numbers.
(8.50 × 1.50). Both 8.5 and 1.5 are decimal numbers. So, we have come across a situation where we need to know how to multiply two decimals. Let us now learn the multiplication of two decimal numbers.
First we find 0.1 × 0.1.
Now, 0.1 =  . So, 0.1 × 0.1 =
. So, 0.1 × 0.1 = 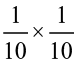 =
=  =
= 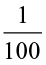 = 0.01.
= 0.01.
Let us see it’s pictorial representation (Fig 2.13)

Fig 2.13
The fraction 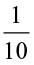 represents 1 part out of 10 equal parts.
represents 1 part out of 10 equal parts.
The shaded part in the picture represents 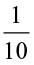 .
.
We know that,
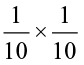 means
means 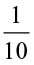 of
of 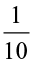 . So, divide this
. So, divide this
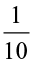 th part into 10 equal parts and take one part out of it.
th part into 10 equal parts and take one part out of it.
Thus, we have, (Fig 2.14).

Fig 2.14
The dotted square is one part out of 10 of the 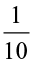 th part. That is, it represents
th part. That is, it represents 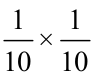 or 0.1 × 0.1.
or 0.1 × 0.1.
Can the dotted square be represented in some other way?
How many small squares do you find in Fig 2.14?
There are 100 small squares. So the dotted square represents one out of 100 or 0.01.
Hence, 0.1 × 0.1 = 0.01.
Note that 0.1 occurs two times in the product. In 0.1 there is one digit to the right of the decimal point. In 0.01 there are two digits (i.e., 1 + 1) to the right of the decimal point.
Let us now find 0.2 × 0.3.
We have, 0.2 × 0.3 = 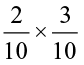
As we did for 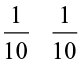 , let us divide the square into 10 equal parts and take three parts out of it, to get
, let us divide the square into 10 equal parts and take three parts out of it, to get 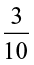 . Again divide each of these three equal parts into 10 equal parts and take two from each. We get
. Again divide each of these three equal parts into 10 equal parts and take two from each. We get 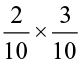 .
.
The dotted squares represent 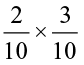 or 0.2 × 0.3. (Fig 2.15)
or 0.2 × 0.3. (Fig 2.15)

Fig 2.15
Since there are 6 dotted squares out of 100, so they also reprsent 0.06.
Thus, 0.2 × 0.3 = 0.06.
Observe that 2 × 3 = 6 and the number of digits to the right of the decimal point in 0.06 is 2 (= 1 + 1).
Check whether this applies to 0.1 × 0.1 also.
Find 0.2 × 0.4 by applying these observations.
While finding 0.1 × 0.1 and 0.2 × 0.3, you might have noticed that first we multiplied them as whole numbers ignoring the decimal point. In 0.1 × 0.1, we found 01 × 01 or 1 × 1. Similarly in 0.2 × 0.3 we found 02 × 03 or 2 × 3.
Then, we counted the number of digits starting from the rightmost digit and moved towards left. We then put the decimal point there. The number of digits to be counted is obtained by adding the number of digits to the right of the decimal point in the decimal numbers that are being multiplied.
Let us now find 1.2 × 2.5.
Multiply 12 and 25. We get 300. Both, in 1.2 and 2.5, there is 1 digit to the right of the decimal point. So, count 1 + 1 = 2 digits from the rightmost digit (i.e., 0) in 300 and move towards left. We get 3.00 or 3.
Find in a similar way 1.5 × 1.6, 2.4 × 4.2.
While multiplying 2.5 and 1.25, you will first multiply 25 and 125. For placing the decimal in the product obtained, you will count 1 + 2 = 3 (Why?) digits starting from the rightmost digit. Thus, 2.5 × 1.25 = 3.225
Find 2.7 × 1.35.
Try These

1. Find: (i) 2.7 × 4 (ii) 1.8 × 1.2 (iii) 2.3 × 4.35
2. Arrange the products obtained in (1) in descending order.
Example 7 The side of an equilateral triangle is 3.5 cm. Find its perimeter.
Solution All the sides of an equilateral triangle are equal.
So, length of each side = 3.5 cm
Thus, perimeter = 3 × 3.5 cm = 10.5 cm
Example 8 The length of a rectangle is 7.1 cm and its breadth is 2.5 cm. What is the area of the rectangle?
Solution Length of the rectangle = 7.1 cm
Breadth of the rectangle = 2.5 cm
Therefore, area of the rectangle = 7.1 × 2.5 cm2 = 17.75 cm2
2.6.1 Multiplication of Decimal Numbers by 10, 100 and 1000
Reshma observed that 2.3 = 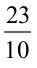 whereas 2.35 =
whereas 2.35 = 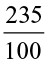 . Thus, she found that depending on the position of the decimal point the decimal number can be converted to a fraction with denominator 10 or 100. She wondered what would happen if a decimal number is multiplied by 10 or 100 or 1000.
. Thus, she found that depending on the position of the decimal point the decimal number can be converted to a fraction with denominator 10 or 100. She wondered what would happen if a decimal number is multiplied by 10 or 100 or 1000.
Let us see if we can find a pattern of multiplying numbers by 10 or 100 or 1000.
Have a look at the table given below and fill in the blanks:

Observe the shift of the decimal point of the products in the table. Here the numbers are multiplied by 10,100 and 1000. In 1.76 × 10 = 17.6, the digits are same i.e., 1, 7 and 6. Do you observe this in other products also? Observe 1.76 and 17.6. To which side has the decimal point shifted, right or left? The decimal point has shifted to the right by one place. Note that 10 has one zero over 1.
In 1.76×100 = 176.0, observe 1.76 and 176.0. To which side and by how many digits has the decimal point shifted? The decimal point has shifted to the right by two places.
Note that 100 has two zeros over one.
Do you observe similar shifting of decimal point in other products also?
So we say, when a decimal number is multiplied by 10, 100 or 1000, the digits in the product are same as in the decimal number but the decimal point in the product is shifted to the right by as, many of places as there are zeros over one.
Try These
Find: (i) 0.3 × 10
(ii) 1.2 × 100
(iii) 56.3 × 1000
Based on these observations we can now say
0.07 × 10 = 0.7, 0.07 × 100 = 7 and 0.07 × 1000 = 70.
Can you now tell 2.97 × 10 = ? 2.97 × 100 = ? 2.97 × 1000 = ?
Can you now help Reshma to find the total amount i.e.,  8.50 × 150, that she has to pay?
8.50 × 150, that she has to pay?
Exercise 2.6

1. Find:
(i) 0.2 × 6 (ii) 8 × 4.6 (iii) 2.71 × 5 (iv) 20.1 × 4
(v) 0.05 × 7 (vi) 211.02 × 4 (vii) 2 × 0.86
2. Find the area of rectangle whose length is 5.7cm and breadth is 3 cm.
3. Find:
(i) 1.3 × 10 (ii) 36.8 × 10 (iii) 153.7 × 10 (iv) 168.07 × 10
(v) 31.1 × 100 (vi) 156.1 × 100 (vii) 3.62 × 100 (viii) 43.07 × 100
(ix) 0.5 × 10 (x) 0.08 × 10 (xi) 0.9 × 100 (xii) 0.03 × 1000
4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?
5. Find:
(i) 2.5 × 0.3 (ii) 0.1 × 51.7 (iii) 0.2 × 316.8 (iv) 1.3 × 3.1
(v) 0.5 × 0.05 (vi) 11.2 × 0.15 (vii) 1.07 × 0.02
(viii) 10.05 × 1.05 (ix) 101.01 × 0.01 (x) 100.01 × 1.1
2.7 Division of Decimal Numbers
 Savita was preparing a design to decorate her classroom. She needed a few coloured strips of paper of length 1.9 cm each. She had a strip of coloured paper of length 9.5 cm. How many pieces of the required length will she get out of this strip? She thought it would be
Savita was preparing a design to decorate her classroom. She needed a few coloured strips of paper of length 1.9 cm each. She had a strip of coloured paper of length 9.5 cm. How many pieces of the required length will she get out of this strip? She thought it would be 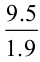 cm. Is she correct?
cm. Is she correct?
Both 9.5 and 1.9 are decimal numbers. So we need to know the division of decimal numbers too!
2.7.1 Division by 10, 100 and 1000
Let us find the division of a decimal number by 10, 100 and 1000.
Consider 31.5 ÷ 10.
31.5 ÷ 10 = 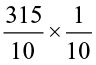 =
= 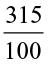 = 3.15
= 3.15
Similarly, 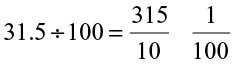
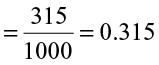
Let us see if we can find a pattern for dividing numbers by 10, 100 or 1000. This may help us in dividing numbers by 10, 100 or 1000 in a shorter way.

Take 31.5 ÷ 10 = 3.15. In 31.5 and 3.15, the digits are same i.e., 3, 1, and 5 but the decimal point has shifted in the quotient. To which side and by how many digits? The decimal point has shifted to the left by one place. Note that 10 has one zero over 1.
Try These

Find: (i) 235.4 ÷ 10
(ii) 235.4 ÷100
(iii) 235.4 ÷ 1000
Consider now 31.5 ÷ 100 = 0.315. In 31.5 and 0.315 the digits are same, but what about the decimal point in the quotient? It has shifted to the left by two places. Note that 100 has two zeros over1.
So we can say that, while dividing a number by 10, 100 or 1000, the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by as many places as there are zeros over 1. Using this observation let us now quickly find: 2.38 ÷ 10 = 0.238, 2.38 ÷ 100 = 0.0238, 2.38 ÷ 1000 = 0.00238
2.7.2 Division of a Decimal Number by a Whole Number
Let us find  . Remember we also write it as 6.4 ÷ 2.
. Remember we also write it as 6.4 ÷ 2.
Try These
(i) 35.7 ÷ 3 = ?;
(ii) 25.5 ÷ 3 = ?
So, 6.4 ÷ 2 = 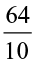 ÷ 2 =
÷ 2 = 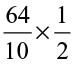 as learnt in fractions..
as learnt in fractions..
= 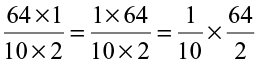 =
= 
Or, let us first divide 64 by 2. We get 32. There is one digit to the right of the decimal point in 6.4. Place the decimal in 32 such that there would be one digit to its right. We get 3.2 again.
To find 19.5 ÷ 5, first find 195 ÷5. We get 39. There is one digit to the right of the decimal point in 19.5. Place the decimal point in 39 such that there would be one digit to its right. You will get 3.9.

Try These
(i) 43.15 ÷ 5 = ?;
(ii) 82.44 ÷ 6 = ?
Now, 12.96 ÷ 4 = 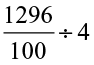
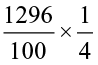 =
= 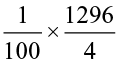 =
= 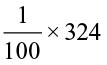 = 3.24
= 3.24
Or, divide 1296 by 4. You get 324. There are two digits to the right of the decimal in 12.96. Making similar placement of the decimal in 324, you will get 3.24.
Note that here and in the next section, we have considered only those divisions in which, ignoring the decimal, the number would be completely divisible by another number to give remainder zero. Like, in 19.5 ÷ 5, the number 195 when divided by 5, leaves remainder zero.
Try These
Find: (i) 15.5 ÷ 5
(ii) 126.35 ÷ 7
However, there are situations in which the number may not be completely divisible by another number, i.e., we may not get remainder zero. For example, 195 ÷ 7. We deal with such situations in later classes.
Thus, 40.86 ÷ 6 = 6.81
Example 9 Find the average of 4.2, 3.8 and 7.6.
Solution The average of 4.2, 3.8 and 7.6 is 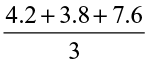 =
= 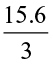 = 5.2.
= 5.2.
2.7.3 Division of a Decimal Number by another Decimal Number
Let us find 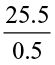 i.e., 25.5 ÷ 0.5.
i.e., 25.5 ÷ 0.5.
We have 25.5 ÷ 0.5 =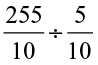 =
= 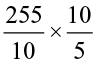 = 51. Thus, 25.5 ÷ 0.5 = 51
= 51. Thus, 25.5 ÷ 0.5 = 51
What do you observe? For 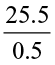 , we find that there is one digit to the right of the decimal in 0.5. This could be converted to whole number by dividing by 10. Accordingly 25.5 was also converted to a fraction by dividing by 10.
, we find that there is one digit to the right of the decimal in 0.5. This could be converted to whole number by dividing by 10. Accordingly 25.5 was also converted to a fraction by dividing by 10.
Or, we say the decimal point was shifted by one place to the right in 0.5 to make it 5. So, there was a shift of one decimal point to the right in 25.5 also to make it 255.
Thus, 22.5 ÷ 1.5 =  =
= 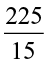 = 15
= 15
Try These
Find: (i) 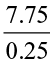 (ii)
(ii) 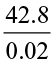 (iii)
(iii) 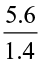
Find 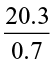 and
and 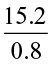 in a similar way.
in a similar way.
Let us now find 20.55 ÷ 1.5.
We can write it is as 205.5 ÷ 15, as discussed above. We get 13.7. Find 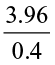 ,
,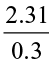 .
.
Consider now,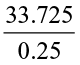 . We can write it as
. We can write it as 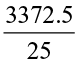 (How?) and we get the quotient as 134.9. How will you find
(How?) and we get the quotient as 134.9. How will you find 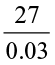 ? We know that 27 can be written as 27.0.
? We know that 27 can be written as 27.0.
So, 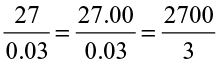 = ?
= ?
Example 10 Each side of a regular polygon is 2.5 cm in length. The perimeter of the polygon is 12.5cm. How many sides does the polygon have?
Solution The perimeter of a regular polygon is the sum of the lengths of all its equal sides = 12.5 cm.
Length of each side = 2.5 cm. Thus, the number of sides = 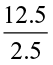 =
= = 5
= 5
The polygon has 5 sides.
Example 11 A car covers a distance of 89.1 km in 2.2 hours. What is the average distance covered by it in 1 hour?
Solution Distance covered by the car = 89.1 km.
Time required to cover this distance = 2.2 hours.
So distance covered by it in 1 hour = 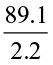 =
=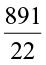 = 40.5 km.
= 40.5 km.
Exercise 2.7

1. Find:
(i) 0.4 ÷ 2 (ii) 0.35 ÷ 5 (iii) 2.48 ÷ 4 (iv) 65.4 ÷ 6
(v) 651.2 ÷ 4 (vi) 14.49 ÷ 7 (vii) 3.96 ÷ 4 (viii) 0.80 ÷ 5
2. Find:
(i) 4.8 ÷ 10 (ii) 52.5 ÷ 10 (iii) 0.7 ÷ 10 (iv) 33.1 ÷ 10
(v) 272.23 ÷ 10 (vi) 0.56 ÷ 10 (vii) 3.97 ÷10
3. Find:
(i) 2.7 ÷ 100 (ii) 0.3 ÷ 100 (iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100 (v) 23.6 ÷100 (vi) 98.53 ÷ 100
4. Find:
(i) 7.9 ÷ 1000 (ii) 26.3 ÷ 1000 (iii) 38.53 ÷ 1000
(iv) 128.9 ÷ 1000 (v) 0.5 ÷ 1000
5. Find:
(i) 7 ÷ 3.5 (ii) 36 ÷ 0.2 (iii) 3.25 ÷ 0.5 (iv) 30.94 ÷ 0.7
(v) 0.5 ÷ 0.25 (vi) 7.75 ÷ 0.25 (vii) 76.5 ÷ 0.15 (viii) 37.8 ÷ 1.4
(ix) 2.73 ÷ 1.3
6. A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre of petrol?
What have We Discussed?
1. We have learnt about fractions and decimals alongwith the operations of addition and subtraction on them, in the earlier class.
2. We now study the operations of multiplication and division on fractions as well as on decimals.
3. We have learnt how to multiply fractions. Two fractions are multiplied by multiplying their numerators and denominators seperately and writing the product as 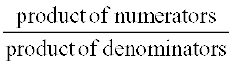 . For example,
. For example, 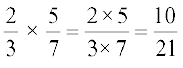 .
.
4. A fraction acts as an operator ‘of’. For example, 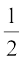 of 2 is
of 2 is 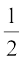 × 2 = 1.
× 2 = 1.
5. (a) The product of two proper fractions is less than each of the fractions that are multiplied.
(b) The product of a proper and an improper fraction is less than the improper fraction and greater than the proper fraction.
(c) The product of two imporper fractions is greater than the two fractions.
6. A reciprocal of a fraction is obtained by inverting it upside down.
7. We have seen how to divide two fractions.
(a) While dividing a whole number by a fraction, we multiply the whole number with the reciprocal of that fraction.
For example, 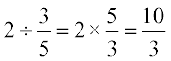
(b) While dividing a fraction by a whole number we multiply the fraction by the reciprocal of the whole number.
For example, 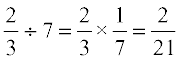
(c) While dividing one fraction by another fraction, we multuiply the first fraction by the reciprocal of the other. So, 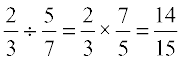 .
.
8. We also learnt how to multiply two decimal numbers. While multiplying two decimal numbers, first multiply them as whole numbers. Count the number of digits to the right of the decimal point in both the decimal numbers. Add the number of digits counted. Put the decimal point in the product by counting the digits from its rightmost place. The count should be the sum obtained earlier.
For example, 0.5 × 0.7 = 0.35
9. To multiply a decimal number by 10, 100 or 1000, we move the decimal point in the number to the right by as many places as there are zeros over 1.
Thus 0.53 × 10 = 5.3, 0.53 × 100 = 53, 0.53 × 1000 = 530
10. We have seen how to divide decimal numbers.
(a) To divide a decimal number by a whole number, we first divide them as whole numbers. Then place the decimal point in the quotient as in the decimal number.
For example, 8.4 ÷ 4 = 2.1
Note that here we consider only those divisions in which the remainder is zero.
(b) To divide a decimal number by 10, 100 or 1000, shift the digits in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
So, 23.9 ÷ 10 = 2.39, 23.9 ÷ 100 = 0 .239, 23.9 ÷ 1000 = 0.0239
(c) While dividing two decimal numbers, first shift the decimal point to the right by equal number of places in both, to convert the divisor to a whole number. Then divide. Thus, 2.4 ÷ 0.2 = 24 ÷ 2 = 12.

