Mathematics - Real Life | Maths 7th STd
Untitled
Chapter 9
Rational Numbers
9.1 Introduction
You began your study of numbers by counting objects around you. The numbers used for this purpose were called counting numbers or natural numbers. They are 1, 2, 3, 4, ... By including 0 to natural numbers, we got the whole numbers, i.e., 0, 1, 2, 3, ... The negatives of natural numbers were then put together with whole numbers to make up integers. Integers are ..., –3, –2, –1, 0, 1, 2, 3, .... We, thus, extended the number system, from natural numbers to whole numbers and from whole numbers to integers.
You were also introduced to fractions. These are numbers of the form  , where the numerator is either 0 or a positive integer and the denominator, a positive integer. You compared two fractions, found their equivalent forms and studied all the four basic operations of addition, subtraction, multiplication and division on them.
, where the numerator is either 0 or a positive integer and the denominator, a positive integer. You compared two fractions, found their equivalent forms and studied all the four basic operations of addition, subtraction, multiplication and division on them.
In this Chapter, we shall extend the number system further. We shall introduce the concept of rational numbers alongwith their addition, subtraction, multiplication and division operations.
9.2 Need for Rational Numbers
Earlier, we have seen how integers could be used to denote opposite situations involving numbers. For example, if the distance of 3 km to the right of a place was denoted by 3, then the distance of 5 km to the left of the same place could be denoted by –5. If a profit of 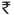 150 was represented by 150 then a loss of
150 was represented by 150 then a loss of 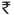 100 could be written as –100.
100 could be written as –100.
There are many situations similar to the above situations that involve fractional numbers. You can represent a distance of 750m above sea level as 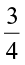 km. Can we represent 750m below sea level in km? Can we denote the distance of
km. Can we represent 750m below sea level in km? Can we denote the distance of 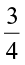 km below sea level by
km below sea level by 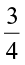 ? We can see
? We can see 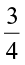 is neither an integer, nor a fractional number. We need to extend our number system to include such numbers.
is neither an integer, nor a fractional number. We need to extend our number system to include such numbers.
9.3 What are Rational Numbers?
The word ‘rational’ arises from the term ‘ratio’. You know that a ratio like 3:2 can also be written as  . Here, 3 and 2 are natural numbers.
. Here, 3 and 2 are natural numbers.
 Similarly, the ratio of two integers p and q (q ≠ 0), i.e., p:q can be written in the form
Similarly, the ratio of two integers p and q (q ≠ 0), i.e., p:q can be written in the form 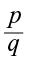 . This is the form in which rational numbers are expressed.
. This is the form in which rational numbers are expressed.
 , where p and q are integers and q ≠ 0.
, where p and q are integers and q ≠ 0.Thus, 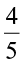 is a rational number. Here, p = 4 and q = 5.
is a rational number. Here, p = 4 and q = 5.
Is 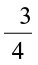 also a rational number? Yes, because p = – 3 and q = 4 are integers.
also a rational number? Yes, because p = – 3 and q = 4 are integers.
• You have seen many fractions like 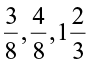 etc. All fractions are rational numbers. Can you say why?
etc. All fractions are rational numbers. Can you say why?
How about the decimal numbers like 0.5, 2.3, etc.? Each of such numbers can be written as an ordinary fraction and, hence, are rational numbers. For example, 0.5 = 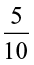 , 0.333 =
, 0.333 = 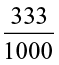 etc.
etc.
Try These

1. Is the number 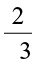 rational? Think about it.
rational? Think about it.
2. List ten rational numbers.
Numerator and Denominator
In  , the integer p is the numerator, and the integer q (≠ 0) is the denominator.
, the integer p is the numerator, and the integer q (≠ 0) is the denominator.
Thus, in  , the numerator is –3 and the denominator is 7.
, the numerator is –3 and the denominator is 7.
Mention five rational numbers each of whose
(a) Numerator is a negative integer and denominator is a positive integer.
(b) Numerator is a positive integer and denominator is a negative integer.
(c) Numerator and denominator both are negative integers.
(d) Numerator and denominator both are positive integers.
• Are integers also rational numbers?
Any integer can be thought of as a rational number. For example, the integer –5 is a rational number, because you can write it as  . The integer 0 can also be written as
. The integer 0 can also be written as 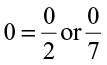 etc. Hence, it is also a rational number.
etc. Hence, it is also a rational number.
Thus, rational numbers include integers and fractions.
Equivalent rational numbers
A rational number can be written with different numerators and denominators. For example, consider the rational number  .
.
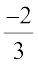 =
= 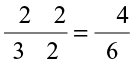 . We see that
. We see that 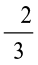 is the same as
is the same as 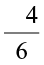 .
.
Also, 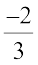 =
=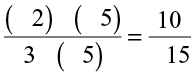 . So,
. So, 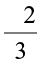 is also the same as
is also the same as  .
.
Thus, 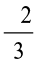 =
= 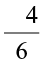 =
=  . Such rational numbers that are equal to each other are said to be equivalent to each other.
. Such rational numbers that are equal to each other are said to be equivalent to each other.
Again,  =
= 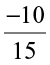 (How?)
(How?)
By multiplying the numerator and denominator of a rational number by the same non zero integer, we obtain another rational number equivalent to the given rational number. This is exactly like obtaining equivalent fractions.
Try These
Fill in the boxes:
(i) 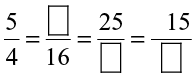
(ii) 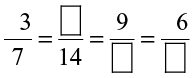
Just as multiplication, the division of the numerator and denominator by the same non zero integer, also gives equivalent rational numbers. For example,
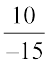 =
= 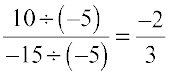 ,
, 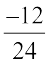 =
= 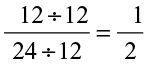
We write  , etc.
, etc.
9.4 Positive and Negative Rational Numbers
Consider the rational number 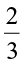 . Both the numerator and denominator of this number are positive integers. Such a rational number is called a positive rational number. So,
. Both the numerator and denominator of this number are positive integers. Such a rational number is called a positive rational number. So, 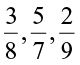 etc. are positive rational number.
etc. are positive rational number.
The numerator of 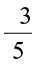 is a negative integer, whereas the denominator is a positive integer. Such a rational number is called a negative rational number. So,
is a negative integer, whereas the denominator is a positive integer. Such a rational number is called a negative rational number. So, 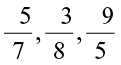 etc. are negative rational numbers.
etc. are negative rational numbers.
Try These
1. Is 5 a positive rational number?
2. List five more positive rational numbers.
Try These
1. Is – 8 a negative rational number?
2. List five more negative rational numbers.
• Is 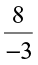 a negative rational number? We know that
a negative rational number? We know that 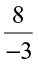 =
= 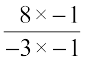 =
= 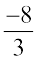 , and
, and  is a negative rational number. So,
is a negative rational number. So, 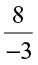 is a negative rational number.
is a negative rational number.
Similarly, 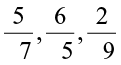 etc. are all negative rational numbers. Note that their numerators are positive and their denominators negative.
etc. are all negative rational numbers. Note that their numerators are positive and their denominators negative.

• The number 0 is neither a positive nor a negative rational number.
• What about 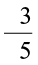 ?
?
You will see that 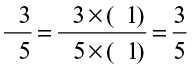 . So,
. So, 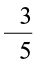 is a positive rational number. Thus,
is a positive rational number. Thus, 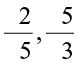 etc. are positive rational numbers.
etc. are positive rational numbers.
Try These

Which of these are negative rational numbers?
(i) 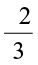 (ii)
(ii) 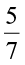 (iii)
(iii) 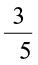 (iv) 0 (v)
(iv) 0 (v) 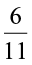 (vi)
(vi) 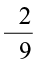
9.5 Rational Numbers on a Number Line
You know how to represent integers on a number line. Let us draw one such number line.
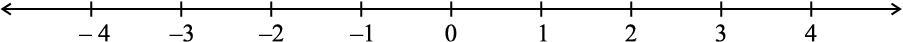
The points to the right of 0 are denoted by + sign and are positive integers. The points to the left of 0 are denoted by – sign and are negative integers.
Representation of fractions on a number line is also known to you.
Let us see how the rational numbers can be represented on a number line.
Let us represent the number 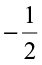 on the number line.
on the number line.
As done in the case of positive integers, the positive rational numbers would be marked on the right of 0 and the negative rational numbers would be marked on the left of 0.
To which side of 0 will you mark  ? Being a negative rational number, it would be marked to the left of 0.
? Being a negative rational number, it would be marked to the left of 0.
You know that while marking integers on the number line, successive integers are marked at equal intervels. Also, from 0, the pair 1 and –1 is equidistant. So are the pairs 2 and –2, 3 and –3.
In the same way, the rational numbers  and
and 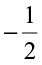 would be at equal distance from 0. We know how to mark the rational number
would be at equal distance from 0. We know how to mark the rational number 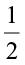 . It is marked at a point which is half the distance between 0 and 1. So,
. It is marked at a point which is half the distance between 0 and 1. So,  would be marked at a point half the distance between 0 and –1.
would be marked at a point half the distance between 0 and –1.
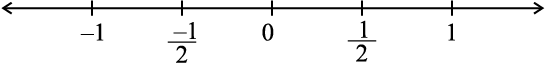
We know how to mark 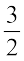 on the number line. It is marked on the right of 0 and lies halfway between 1 and 2. Let us now mark
on the number line. It is marked on the right of 0 and lies halfway between 1 and 2. Let us now mark 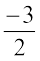 on the number line. It lies on the left of 0 and is at the same distance as
on the number line. It lies on the left of 0 and is at the same distance as 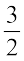 from 0.
from 0.
In decreasing order, we have, 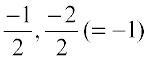 ,
, 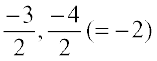 . This shows that
. This shows that 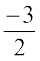 lies between – 1 and – 2. Thus,
lies between – 1 and – 2. Thus, 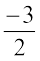 lies halfway between – 1 and – 2.
lies halfway between – 1 and – 2.
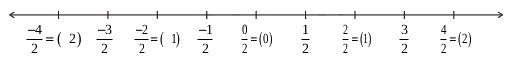
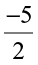 and
and 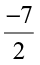 in a similar way.
in a similar way.Similarly, 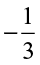 is to the left of zero and at the same distance from zero as
is to the left of zero and at the same distance from zero as 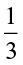 is to the right. So as done above,
is to the right. So as done above, 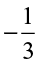 can be represented on the number line. Once we know how to represent
can be represented on the number line. Once we know how to represent 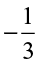 on the number line, we can go on representing
on the number line, we can go on representing 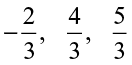 and so on. All other rational numbers with different denominators can be represented in a similar way.
and so on. All other rational numbers with different denominators can be represented in a similar way.
9.6 Rational Numbers in Standard Form

Observe the rational numbers 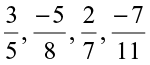 .
.
The denominators of these rational numbers are positive integers and 1 is the only common factor between the numerators and denominators. Further, the negative sign occurs only in the numerator.
Such rational numbers are said to be in standard form.
A rational number is said to be in the standard form if its denominator is a positive integer and the numerator and denominator have no common factor other than 1.
If a rational number is not in the standard form, then it can be reduced to the standard form.
Recall that for reducing fractions to their lowest forms, we divided the numerator and the denominator of the fraction by the same non zero positive integer. We shall use the same method for reducing rational numbers to their standard form.
EXAMPLE 1 Reduce  to the standard form.
to the standard form.
SOLUTION We have, 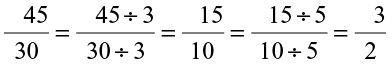
We had to divide twice. First time by 3 and then by 5. This could also be done as

In this example, note that 15 is the HCF of 45 and 30.
Thus, to reduce the rational number to its standard form, we divide its numerator and denominator by their HCF ignoring the negative sign, if any. (The reason for ignoring the negative sign will be studied in Higher Classes)
If there is negative sign in the denominator, divide by ‘– HCF’.
EXAMPLE 2 Reduce to standard form:

(i) 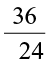 (ii)
(ii) 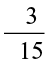
(i) The HCF of 36 and 24 is 12.
Thus, its standard form would be obtained by dividing by –12.
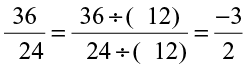
(ii) The HCF of 3 and 15 is 3.
Thus, 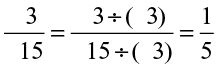
Try These

Find the standard form of (i) 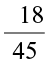 (ii)
(ii) 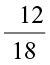
9.7 Comparison of Rational Numbers
We know how to compare two integers or two fractions and tell which is smaller or which is greater among them. Let us now see how we can compare two rational numbers.
• Two positive rational numbers, like 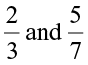 can be compared as studied earlier in the case of fractions.
can be compared as studied earlier in the case of fractions.
• Mary compared two negative rational numbers 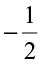 and
and 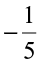 using number line. She knew that the integer which was on the right side of the other integer, was the greater integer.
using number line. She knew that the integer which was on the right side of the other integer, was the greater integer.
For example, 5 is to the right of 2 on the number line and 5 > 2. The integer – 2 is on the right of – 5 on the number line and – 2 > – 5.
She used this method for rational numbers also. She knew how to mark rational numbers on the number line. She marked  and
and 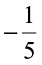 as follows:
as follows:
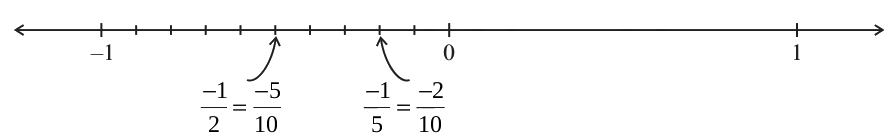
Has she correctly marked the two points? How and why did she convert 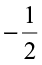 to
to 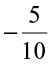 and
and 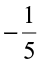 to
to 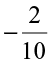 ? She found that
? She found that 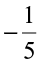 is to the right of
is to the right of 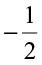 . Thus,
. Thus, 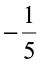 >
>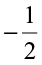 or
or 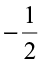 <
< .
.
Can you compare 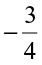 and
and 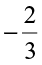 ?
? 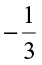 and
and 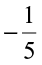 ?
?
We know from our study of fractions that  <
<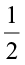 . And what did Mary get for
. And what did Mary get for 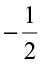 and
and 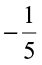 ? Was it not exactly the opposite?
? Was it not exactly the opposite?
You will find that, 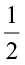 >
>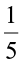 but
but 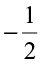 <
<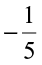 .
.
Do you observe the same for 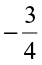 ,
, 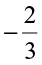 and
and 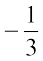 ,
, 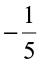 ?
?
Mary remembered that in integers she had studied 4 > 3 but – 4 < –3, 5 > 2 but –5 < –2 etc.

• The case of pairs of negative rational numbers is similar. To compare two negative rational numbers, we compare them ignoring their negative signs and then reverse the order.
For example, to compare  and
and 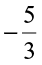 , we first compare
, we first compare 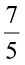 and
and 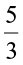 .
.
We get 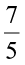 <
< 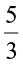 and conclude that
and conclude that 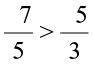 .
.
Take five more such pairs and compare them.
Which is greater  or
or 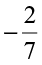 ?;
?; 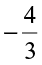 or
or 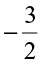 ?
?
• Comparison of a negative and a positive rational number is obvious. A negative rational number is to the left of zero whereas a positive rational number is to the right of zero on a number line. So, a negative rational number will always be less than a positive rational number.
Thus, 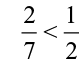 .
.
• To compare rational numbers  reduce them to their standard forms and then compare them.
reduce them to their standard forms and then compare them.
EXAMPLE 3 Do 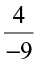 and
and 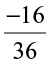 represent the same rational number?
represent the same rational number?
SOLUTION Yes, because 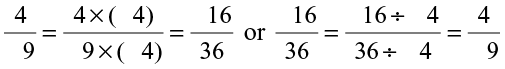 .
.
9.8 Rational Numbers Between Two Rational Numbers
Reshma wanted to count the whole numbers between 3 and 10. From her earlier classes, she knew there would be exactly 6 whole numbers between 3 and 10. Similarly, she wanted to know the total number of integers between –3 and 3. The integers between –3 and 3 are –2, –1, 0, 1, 2. Thus, there are exactly 5 integers between –3 and 3.
Are there any integers between –3 and –2? No, there is no integer between –3 and –2. Between two successive integers the number of integers is 0.
Thus, we find that number of integers between two integers are limited (finite).
Will the same happen in the case of rational numbers also?
 Reshma took two rational numbers
Reshma took two rational numbers 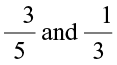 .
.
She converted them to rational numbers with same denominators.
So 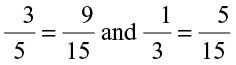
We have 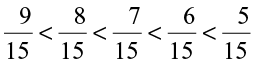 or
or 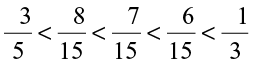
She could find rational numbers 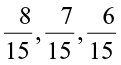 between
between 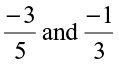 .
.
Are the numbers 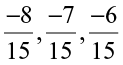 the only rational numbers between
the only rational numbers between 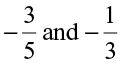 ?
?
We have 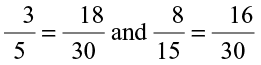
And 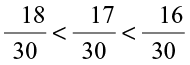 . i.e.,
. i.e., 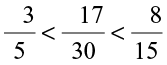
Hence 
So, we could find one more rational number between 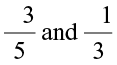 .
.
By using this method, you can insert as many rational numbers as you want between two rational numbers.
For example, 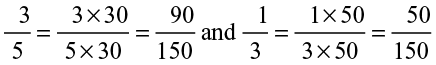

We get 39 rational numbers 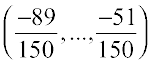 between
between 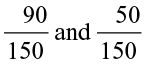 i.e., between
i.e., between  . You will find that the list is unending.
. You will find that the list is unending.
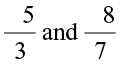 ?
?We can find unlimited number of rational numbers between any two rational numbers.
Try These
Find five rational numbers between 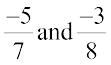 .
.
EXAMPLE 4 List three rational numbers between – 2 and – 1.
SOLUTION Let us write –1 and –2 as rational numbers with denominator 5. (Why?)
We have, –1 = 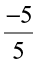 and –2 =
and –2 = 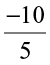
So, 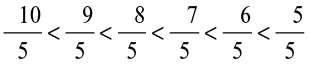 or
or 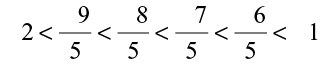
The three rational numbers between –2 and –1 would be, 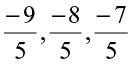
(You can take any three of 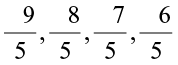 )
)
EXAMPLE 5 Write four more numbers in the following pattern:
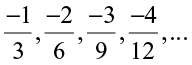

SOLUTION We have,
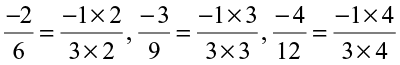
or 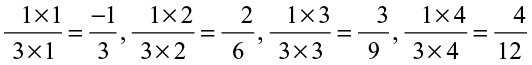
Thus, we observe a pattern in these numbers.
The other numbers would be 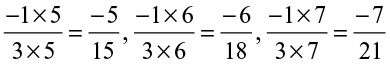 .
.
Exercise 9.1
 1. List five rational numbers between:
1. List five rational numbers between:
(i) –1 and 0 (ii) –2 and –1 (iii)  (iv)
(iv) 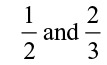
2. Write four more rational numbers in each of the following patterns:
(i) 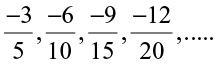 (ii)
(ii) 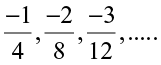
(iii) 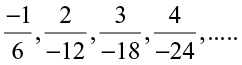 (iv)
(iv) 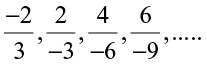
3. Give four rational numbers equivalent to:
(i) 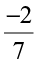 (ii)
(ii) 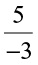 (iii)
(iii) 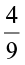
4. Draw the number line and represent the following rational numbers on it:
(i) 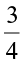 (ii)
(ii) 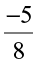 (iii)
(iii) 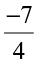 (iv)
(iv) 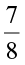
5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
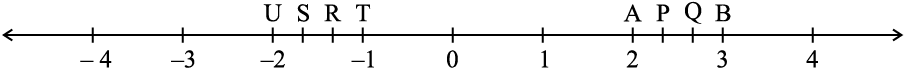
6. Which of the following pairs represent the same rational number?
(i) 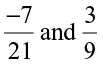 (ii)
(ii) 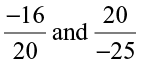 (iii)
(iii) 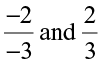
(iv) 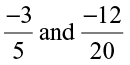 (v)
(v) 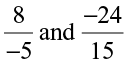 (vi)
(vi) 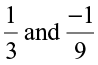
(vii) 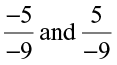
7. Rewrite the following rational numbers in the simplest form:
(i) 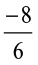 (ii)
(ii) 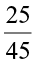 (iii)
(iii) 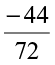 (iv)
(iv) 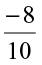
8. Fill in the boxes with the correct symbol out of >, <, and =.
(i) 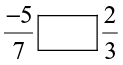 (ii)
(ii)  (iii)
(iii) 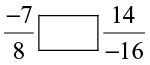
(iv)  (v)
(v)  (vi)
(vi) 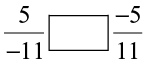
(vii) 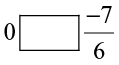
9. Which is greater in each of the following:
(i) 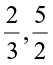 (ii)
(ii) 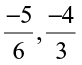 (iii)
(iii) 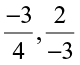
(iv) 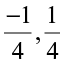 (v)
(v) 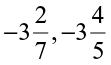
10. Write the following rational numbers in ascending order:
(i) 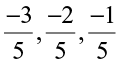 (ii)
(ii) 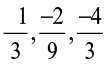 (iii)
(iii) 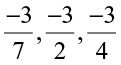
9.9 Operations on Rational Numbers
You know how to add, subtract, multiply and divide integers as well as fractions. Let us now study these basic operations on rational numbers.
9.9.1 Addition
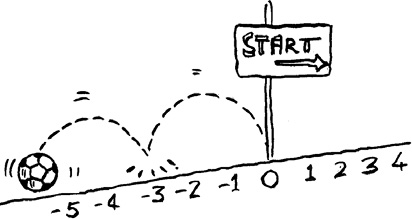
• Let us add two rational numbers with same denominators, say 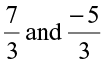 .
.
We find 
On the number line, we have:

The distance between two consecutive points is 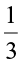 . So adding
. So adding 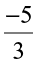 to
to 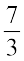 will mean, moving to the left of
will mean, moving to the left of 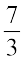 , making 5 jumps.Where do we reach? We reach at
, making 5 jumps.Where do we reach? We reach at 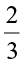 . So,
. So, 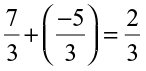 .
.
Let us now try this way: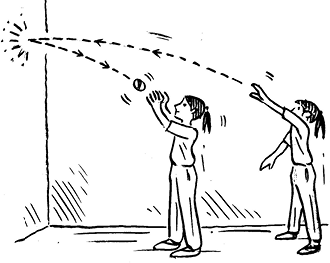
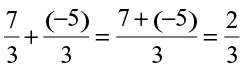
We get the same answer.
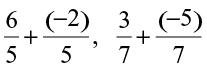 in both ways and check if you get the same answers.
in both ways and check if you get the same answers.Similarly, 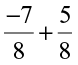 would be
would be

What do you get?
Also, 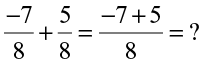 Are the two values same?
Are the two values same?
Try These
Find: 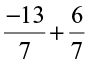 ,
, 
So, we find that while adding rational numbers with same denominators, we add the numerators keeping the denominators same.
Thus, 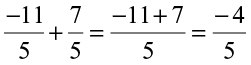
• How do we add rational numbers with different denominators? As in the case of fractions, we first find the LCM of the two denominators. Then, we find the equivalent rational numbers of the given rational numbers with this LCM as the denominator. Then, add the two rational numbers.
For example, let us add  .
.
LCM of 5 and 3 is 15.
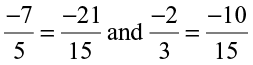
Thus, 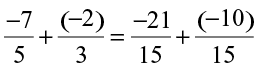
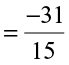
Try These
Find:
(i) 
(ii) 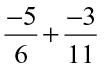
Additive Inverse
What will be 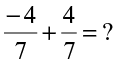
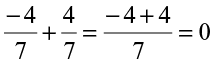 . Also,
. Also,  .
.
 Similarly,
Similarly, 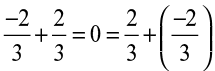 .
.
In the case of integers, we call – 2 as the additive inverse of 2 and 2 as the additive inverse of – 2.
For rational numbers also, we call 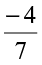 as the additive inverse of
as the additive inverse of 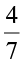 and
and 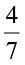 as the additive inverse of
as the additive inverse of 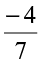 . Similarly,
. Similarly, 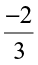 is the additive inverse of
is the additive inverse of 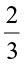 and
and 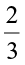 is the additive inverse of
is the additive inverse of 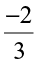 .
.
Try These
 What will be the additive inverse of
What will be the additive inverse of 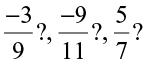
EXAMPLE 6 Satpal walks 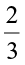 km from a place P, towards east and then from there
km from a place P, towards east and then from there 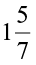 km towards west. Where will he be now from P?
km towards west. Where will he be now from P?
SOLUTION Let us denote the distance travelled towards east by positive sign. So, the distances towards west would be denoted by negative sign.
Thus, distance of Satpal from the point P would be
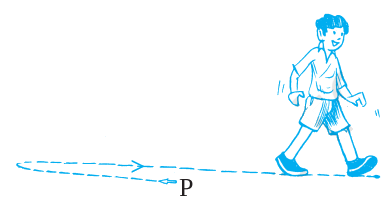
 =
= 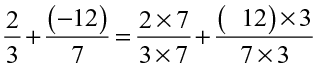
= 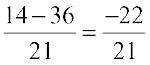
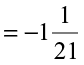
Since it is negative, it means Satpal is at a distance 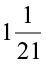 km towards west of P.
km towards west of P.
9.9.2 Subtraction
Savita found the difference of two rational numbers 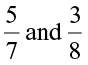 in this way:
in this way:
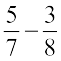 =
= 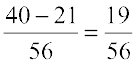
Farida knew that for two integers a and b she could write a – b = a + (– b)
She tried this for rational numbers also and found, 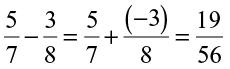 .
.
Both obtained the same difference.
Try to find 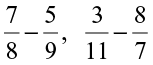 in both ways. Did you get the same answer?
in both ways. Did you get the same answer?
So, we say while subtracting two rational numbers, we add the additive inverse of the rational number that is being subtracted, to the other rational number.
Thus, 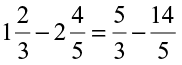 =
=  + additive inverse of
+ additive inverse of 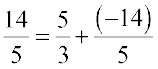
 .
.
Try These
Find:
(i) 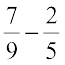 (ii)
(ii) 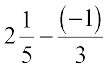

 additive inverse of
additive inverse of 
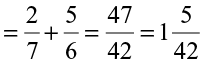
9.9.3 Multiplication
Let us multiply the rational number 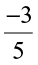 by 2, i.e., we find
by 2, i.e., we find 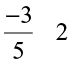 .
.
On the number line, it will mean two jumps of 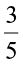 to the left.
to the left.

Where do we reach? We reach at 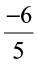 . Let us find it as we did in fractions.
. Let us find it as we did in fractions.
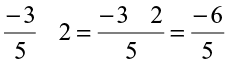
We arrive at the same rational number.
Find 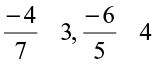 using both ways. What do you observe?
using both ways. What do you observe?
So, we find that while multiplying a rational number by a positive integer, we multiply the numerator by that integer, keeping the denominator unchanged.
Let us now multiply a rational number by a negative integer,
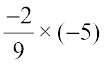 =
= 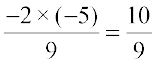

Try These
What will be

Remember, –5 can be written as  .
.
So, 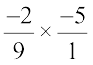 =
= 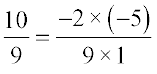
Similarly,  =
= 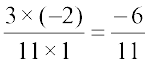
Based on these observations, we find that, 
So, as we did in the case of fractions, we multiply two rational numbers in the following way:
Try These
Find:
(i) 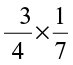
(ii) 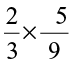
Step 1 Multiply the numerators of the two rational numbers.
Step 2 Multiply the denominators of the two rational numbers.
Step 3 Write the product as 
Thus, 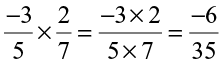 .
.
Also, 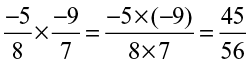
9.9.4 Division
We have studied reciprocals of a fraction earlier. What is the reciprocal of 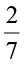 ? It will be
? It will be 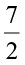 . We extend this idea of reciprocals to rational numbers also.
. We extend this idea of reciprocals to rational numbers also.
The reciprocal of 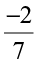 will be
will be 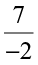 i.e.,
i.e., 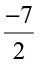 ; that of
; that of 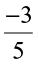 would be
would be 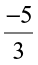 .
.
Try These

What will be the reciprocal of 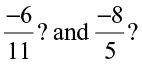
Product of reciprocals
The product of a rational number with its reciprocal is always 1.
For example, 
= 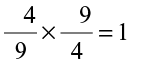
Similarly, 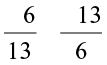 = 1
= 1
Try some more examples and confirm this observation.
Savita divided a rational number 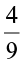 by another rational number
by another rational number 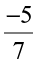 as,
as,
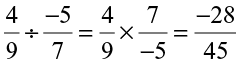 .
.
She used the idea of reciprocal as done in fractions.
Arpit first divided 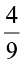 by
by 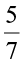 and got
and got 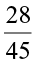 .
.
He finally said 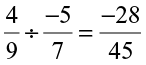 . How did he get that?
. How did he get that?
He divided them as fractions, ignoring the negative sign and then put the negative sign in the value so obtained.
Both of them got the same value 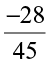 . Try dividing
. Try dividing  by
by  both ways and see if you get the same answer.
both ways and see if you get the same answer.
This shows, to divide one rational number by the other rational number we multiply the rational number by the reciprocal of the other.
Thus, 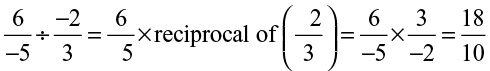
Try These

Find: (i) 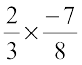 (ii)
(ii) 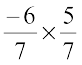
Exercise 9.2
 1. Find the sum:
1. Find the sum:
(i)  (ii)
(ii) 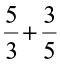 (iii)
(iii) 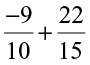
(iv) 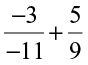 (v)
(v) 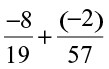 (vi)
(vi) 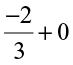
(vii) 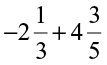
2. Find
(i) 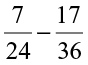 (ii)
(ii)  (iii)
(iii) 
(iv)  (v)
(v) 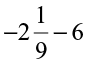
3. Find the product:
(i)  (ii)
(ii) 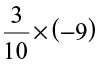 (iii)
(iii) 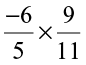
(iv)  (v)
(v) 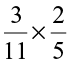 (vi)
(vi) 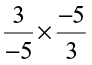
4. Find the value of:
(i) 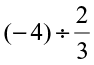 (ii)
(ii) 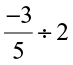 (iii)
(iii) 
(iv) 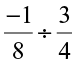 (v)
(v) 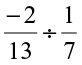 (vi)
(vi) 
(vii) 
What have we discussed?
1. A number that can be expressed in the form 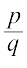 , where p and q are integers and
, where p and q are integers and
q 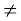 0, is called a rational number. The numbers
0, is called a rational number. The numbers 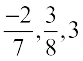 etc. are rational numbers.
etc. are rational numbers.
2. All integers and fractions are rational numbers.
3. If the numerator and denominator of a rational number are multiplied or divided by a non-zero integer, we get a rational number which is said to be equivalent to the given rational number. For example 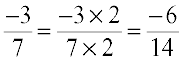 . So, we say
. So, we say  is the equivalent form of
is the equivalent form of 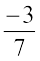 . Also note that
. Also note that 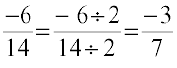 .
.
4. Rational numbers are classified as Positive and Negative rational numbers. When the numerator and denominator, both, are positive integers, it is a positive rational number. When either the numerator or the denominator is a negative integer, it is a negative rational number. For example, 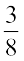 is a positive rational number whereas
is a positive rational number whereas 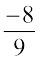 is a negative rational number.
is a negative rational number.
5. The number 0 is neither a positive nor a negative rational number.
6. A rational number is said to be in the standard form if its denominator is a positive integer and the numerator and denominator have no common factor other than 1. The numbers 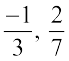 etc. are in standard form.
etc. are in standard form.
7. There are unlimited number of rational numbers between two rational numbers.
8. Two rational numbers with the same denominator can be added by adding their numerators, keeping the denominator same. Two rational numbers with different denominators are added by first taking the LCM of the two denominators and then converting both the rational numbers to their equivalent forms having the LCM as the denominator. For example,  . Here, LCM of 3 and 8 is 24.
. Here, LCM of 3 and 8 is 24.
9. While subtracting two rational numbers, we add the additive inverse of the rational number to be subtracted to the other rational number.
Thus, 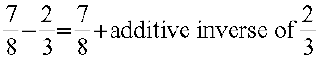 =
= 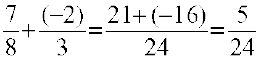 .
.
10. To multiply two rational numbers, we multiply their numerators and denominators separately, and write the product as 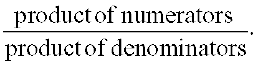
11. To divide one rational number by the other non-zero rational number, we multiply the rational number by the reciprocal of the other. Thus,
 × (reciprocal of
× (reciprocal of 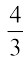 )
) 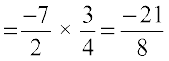 .
.


