Summary: Ratio and Proportion (7th Grade Math)

Ratio and Proportion are tools used to compare quantities. A ratio shows how two numbers relate to each other in terms of size. Proportion is used when two ratios are equal.

Key Points

• Ratio: A comparison between two quantities using division. It is denoted by a colon, e.g., 3:1 means that for every 3 of one quantity, there is 1 of the other.
• Proportion: A proportion occurs when two ratios are equivalent. For example, if 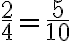$\frac{2}{4} = \frac{5}{10}$, the two ratios are in proportion.
• Equivalent Ratios: Two ratios are equivalent if they simplify to the same fraction.
• Unitary Method: A method where you first calculate the value of one unit and then find the value of the required number of units.

Illustrations

Example 1: If 3 pens cost ₹15, and 10 pens cost ₹50, both ratios (3:10 and 15:50) are equivalent, meaning the cost per pen is the same.

Example 2: In a class, if there are 20 boys and 40 girls, the ratio of boys to girls is 20:40, which simplifies to 1:2.

Short Answer Questions

1. What is a ratio?
A ratio compares two quantities by division, showing how many times one value contains another.

2. How do you represent a proportion?
A proportion shows two equal ratios. For example, 2:3 :: 4:6 means 2 is to 3 as 4 is to 6.

3. What is the unitary method?
The unitary method involves finding the value of a single unit and then using it to find the value of multiple units.

15 Problems with Solutions

Problem 1

Question: Find the ratio of 90 cm to 1.5 meters.

Solution: First, convert both quantities to the same unit (1.5 meters = 150 cm). Now, the ratio is 90:150, which simplifies to 3:5.

Problem 2

Question: There are 45 workers in an office, 25 of whom are women. Find the ratio of women to men.

Solution: Number of men = 45 - 25 = 20. Therefore, the ratio of women to men is 25:20, which simplifies to 5:4.

Problem 3

Question: If 2 pens cost ₹30, how much do 5 pens cost?

Solution: Use the unitary method: Cost of 1 pen = ₹30 ÷ 2 = ₹15. Cost of 5 pens = ₹15 × 5 = ₹75.

Problem 4

Question: Find the ratio of 6:4 and provide two equivalent ratios.

Solution: Simplify 6:4 to 3:2. Two equivalent ratios are 12:8 and 9:6 (both found by multiplying/dividing the terms by the same number).

Problem 5

Question: A car travels 90 km in 2.5 hours. How long does it take to travel 30 km at the same speed?

Solution: Use the unitary method: Time to travel 1 km = 2.5 hours ÷ 90 = 1/36 hours. Time to travel 30 km = 30 × (1/36) = 50 minutes.

Problem 6

Question: Divide ₹60 between two people in the ratio 2:3.

Solution: Total parts = 2 + 3 = 5. One part = ₹60 ÷ 5 = ₹12. Person 1 receives ₹12 × 2 = ₹24, Person 2 receives ₹12 × 3 = ₹36.

Problem 7

Question: Find if 15:45 and 5:15 are equivalent ratios.

Solution: Simplify both: 15:45 simplifies to 1:3, and 5:15 also simplifies to 1:3. Therefore, they are equivalent ratios.

Problem 8

Question: If the cost of 6 cans of juice is ₹210, what is the cost of 4 cans?

Solution: Cost of 1 can = ₹210 ÷ 6 = ₹35. Cost of 4 cans = ₹35 × 4 = ₹140.

Problem 9

Question: If 10 pens cost ₹100, what is the cost of 7 pens?

Solution: Cost of 1 pen = ₹100 ÷ 10 = ₹10. Cost of 7 pens = ₹10 × 7 = ₹70.

Problem 10

Question: A truck requires 108 litres of diesel to cover 594 km. How much diesel will it need to cover 1650 km?

Solution: Use the unitary method: Diesel per km = 108 ÷ 594 = 0.18 litres/km. For 1650 km = 0.18 × 1650 = 297 litres.

Problem 11

Question: Are the ratios 16:24 and 20:30 in proportion?

Solution: Simplify 16:24 to 2:3 and 20:30 to 2:3. Since they are equal, they are in proportion.

Problem 12

Question: In a class, 6 students like football, 12 like cricket, and 12 like tennis. Find the ratio of football to tennis lovers.

Solution: The ratio is 6:12, which simplifies to 1:2.

Problem 13

Question: If Seema earns ₹1,50,000 and saves ₹50,000, what is the ratio of earnings to savings?

Solution: The ratio is ₹1,50,000:₹50,000, which simplifies to 3:1.

Problem 14

Question: If the cost of 5 kg of wheat is ₹91.50, what is the cost of 8 kg?

Solution: Cost per kg = ₹91.50 ÷ 5 = ₹18.3. Cost of 8 kg = ₹18.3 × 8 = ₹146.40.

Problem 15

Question: If a scooter uses 2 litres of petrol to travel 80 km, how much petrol is needed for 120 km?

Solution: Petrol per km = 2 ÷ 80 = 0.025 litres/km. For 120 km = 0.025 × 120 = 3 litres.

Mnemonics

• RAP: To remember the basics of Ratio and Proportion – Ratio, Algebra, Proportion.